Balancing Accuracy and Recall in Hebbian and Quantum-inspired Learning Models
Abstract
Introduction
This study investigates integrating quantum-inspired learning models with traditional Hebbian learning within neural networks, comparing their performance in learning efficiency, generalization, stability, and robustness. Traditional Hebbian models are biologically plausible but often struggle with stability, scalability, and adaptability. In contrast, quantum-inspired models leverage quantum mechanics principles like superposition and entanglement to enhance neural network performance potentially.
Methods
The simulations were conducted using a neural network comprising 1,000 neurons and 100 patterns across 10 instances. The key parameters included a fixed decay rate of 0.005, 80% excitatory neurons, and 10% fixed connectivity. The study varied learning rates (0.01, 0.05, 0.1) and thresholds (0.3, 0.5, 0.7) to assess different parameter settings. The performance metrics evaluated included accuracy, precision, recall, and F1-Score.
Results
The results showed that quantum-inspired models achieved significantly higher accuracy and precision, enhancing their reliability in class prediction and reducing false positives. Conversely, Hebbian models excelled in recall and F1-Score, effectively identifying positive cases and balancing precision and recall. Additionally, quantum-inspired models demonstrated greater stability, robustness, and consistent performance across varying parameters.
Conclusion
Quantum-inspired models offer notable improvements in learning efficiency, generalization, stability, and robustness, while Hebbian models perform better in recall and F1-Score. These findings suggest the potential for hybrid models that combine the strengths of both approaches, aiming for more balanced and efficient learning systems. Future research should explore these hybrid models to enhance performance across diverse artificial intelligence applications. Supplementary materials include the complete R code used, enabling replication and further investigation of the results.
1. INTRODUCTION
The study of neural networks has profoundly advanced the field of artificial intelligence, driven by a fundamental question: how can artificial systems emulate the processes of learning and memory seen in biological organisms? Central to this inquiry is the development of learning algorithms that enable networks to adapt, generalize, and execute complex tasks efficiently and precisely [1-5]. Hebbian learning has historically been a cornerstone among these algorithms, offering a biologically plausible framework for modeling associative memory [6-8]. However, as computational demands have grown, the limitations of Hebbian learning —particularly its scalability and adaptability—have become increasingly apparent [9]. These constraints have inspired the search for innovative approaches, including integrating principles from quantum mechanics to redefine how neural networks learn and process information.
This article introduces a novel quantum-inspired learning framework that transcends the constraints of traditional methods [10-12]. The proposed approach offers new pathways for encoding, processing, and generalizing information by leveraging quantum mechanics concepts such as superposition and entanglement [13, 14]. Unlike conventional learning models, which rely on deterministic updates to synaptic weights, this framework incorporates probabilistic mechanisms that enable neural networks to explore multiple solutions simultaneously [15, 16]. This innovation enhances the efficiency and robustness of learning, addressing many of the challenges inherent in conventional methods while expanding the potential for future advancements in neural computation.
1.1. The Role of Hebbian Learning in Neural Networks
Artificial neural networks are computational systems inspired by the architecture and function of biological neural systems [17-20]. They rely on algorithms to adjust the strength of synaptic connections, or weights, between artificial neurons. Hebbian learning, introduced in 1949, has been instrumental in this domain due to its simplicity and alignment with biological processes [21]. It operates on the rule that simultaneous activation of two neurons strengthens their connection—a principle encapsulated in the phrase, “cells that fire together wire together.”
Hebbian learning has been particularly effective in associative memory systems, where neural networks store and retrieve patterns based on incomplete or noisy inputs. For example, Hopfield networks, a class of associative memory models, rely heavily on Hebbian-like updates to recall stored patterns [22]. These models simulate how humans retrieve entire memories from partial cues, reflecting the real-world utility of Hebbian mechanisms.
Despite its foundational role, Hebbian learning exhibits critical shortcomings when applied to modern, complex computational tasks. Its simplicity, which makes it biologically plausible, also limits its adaptability. Traditional Hebbian models are prone to overfitting and memorizing specific patterns without effectively generalizing them to new or distorted inputs. This rigidity undermines their performance in dynamic and high-dimensional environments, where adaptability and scalability are paramount [23, 24].
The limitations of Hebbian learning extend beyond its inability to generalize. One significant drawback is the absence of mechanisms to regulate synaptic growth effectively. Without such regulation, Hebbian learning often leads to unstable weight dynamics or saturation, where synapses reach their maximum strength and fail to adapt. These phenomena compromise the model's stability, particularly when data distributions change over time [25-27].
Additionally, Hebbian learning struggles to handle noisy or incomplete data, a frequent occurrence in real-world applications. Its reliance on fixed update rules makes it less responsive to variations in input patterns, reducing its robustness in dynamic scenarios. In high-dimensional datasets, the computational demands of Hebbian learning increase exponentially, making it less feasible for large-scale tasks [28].
These limitations have prompted the exploration of alternative frameworks that can overcome the rigidity of Hebbian learning while preserving its strengths. Among the most promising approaches is incorporating quantum mechanics principles to enhance the flexibility and efficiency of neural computation.
1.2. A Quantum-inspired Framework for Neural Networks
The quantum-inspired learning framework proposed in this study addresses the limitations of Hebbian learning by leveraging core principles of quantum mechanics [29]. Traditionally associated with physics, quantum mechanics provides a fundamentally different paradigm for representing and processing information. Concepts such as superposition, entanglement, and probabilistic states offer unique advantages for efficiently encoding complex relationships between variables and exploring solution spaces [30-33].
1.2.1. Superposition in Neural Networks
Superposition, a foundational principle of quantum mechanics, allows systems to exist in multiple states simultaneously. When applied to neural networks, this property enables the representation of information probabilistically, where multiple potential solutions are considered concurrently. This contrasts with traditional deterministic models, which sequentially explore individual solutions. By evaluating many possibilities in parallel, quantum-inspired models accelerate the learning process and reduce the risk of becoming trapped in local minima—suboptimal points in the optimization landscape. For example, superposition in tasks such as pattern recognition allows a quantum-inspired neural network to evaluate multiple feature combinations simultaneously. This parallelism enhances the network's ability to identify patterns in high-dimensional data, improving accuracy and efficiency [13, 34, 35].
1.2.2. Entanglement and Connectivity
Entanglement, another core quantum principle, introduces deep correlations between system elements that persist regardless of distance [36, 37]. In neural networks, entanglement-inspired mechanisms can strengthen the connectivity between neurons, fostering a more integrated and holistic learning process. By capturing complex dependencies among features, entanglement enhances the network's ability to generalize from limited training data, making it particularly valuable in applications involving incomplete or noisy inputs [38-40].
1.2.3. Probabilistic Learning
The probabilistic nature of quantum-inspired learning offers distinct advantages over traditional deterministic approaches. Conventional models rely on fixed update rules for adjusting synaptic weights, which can lead to rigid learning pathways and poor adaptability. In contrast, quantum-inspired models use probabilistic updates, introducing variability that enables broader solution space exploration [41, 42]. This stochastic approach reduces the likelihood of converging prematurely to suboptimal solutions, resulting in more robust learning outcomes.
1.3. Objectives of This Study
This research evaluates the comparative performance of traditional Hebbian learning models and quantum-inspired models within neural networks. The study explores key dimensions of performance, including:
1. Learning Efficiency: Assessing how quickly and accurately each model learns patterns.
2. Generalization Capabilities: Examining the adaptability of models to new or distorted inputs, reflecting their robustness to novel scenarios.
3. Stability and Robustness: Investigating the consistency of model performance under varying parameter settings, such as learning rates and activation thresholds.
4. Trade-offs in Performance Metrics: Exploring the relationships between precision, recall, and overall accuracy to identify the strengths and limitations of each approach.
5. Through systematic simulations and quantitative analysis, this study seeks to illuminate the unique contributions of quantum-inspired learning to neural computation.
The implications of this research extend beyond theoretical exploration. The proposed quantum-inspired framework has practical applications requiring high efficiency, scalability, and adaptability. For example, tasks such as image recognition, natural language processing, and medical diagnostics often involve noisy and high-dimensional data, where traditional methods struggle to perform reliably [43]. The probabilistic and parallel nature of quantum-inspired models makes them particularly suited to these challenges.
Moreover, the insights gained from this study contribute to the broader understanding of neural computation, highlighting the potential for interdisciplinary approaches that integrate quantum mechanics principles into artificial intelligence. By addressing the limitations of traditional learning models, this research paves the way for developing more versatile and efficient neural networks capable of tackling complex real-world tasks.
2. METHODS
2.1. Study Design
This study aims to compare the performance of traditional Hebbian learning models with Quantum-inspired models in neural network simulations. A balanced approach to parameter selection was employed, combining fixed and varying parameters to maintain computational feasibility while providing meaningful insights. The computational cost of neural network simulations increases exponentially with the number of varying parameters [44]. By fixing the number of neurons and patterns, we maintain a manageable computation load while varying only the learning rate and threshold, which reduces the number of parameter combinations, making the simulation feasible on standard computational resources (The simulations were conducted using R programming on a personal laptop with a Ryzen 7 AMD processor and 16 GB of RAM, and took over 14 hours to complete).
2.2. Model Construction
Constructing the Hebbian and Quantum-inspired learning models is fundamental to this study (Table 1).
| Model | Description | Formula |
|---|---|---|
| Hebbian Learning Model | Weight Initialization | wij ∼ N (0,0.1) |
| Connectivity Mask | 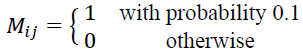 |
|
| Proportion of Excitatory Neurons | Excitatory neurons=0.8×N | |
| Quantum-Inspired Model | Quantum State Initialization | qij∼ N (0,1) + i N (0,1) |
| Quantum Encoding | ΔQ = α⋅(p⋅pH + ϵ) | |
| Normalization | 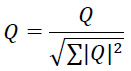 |
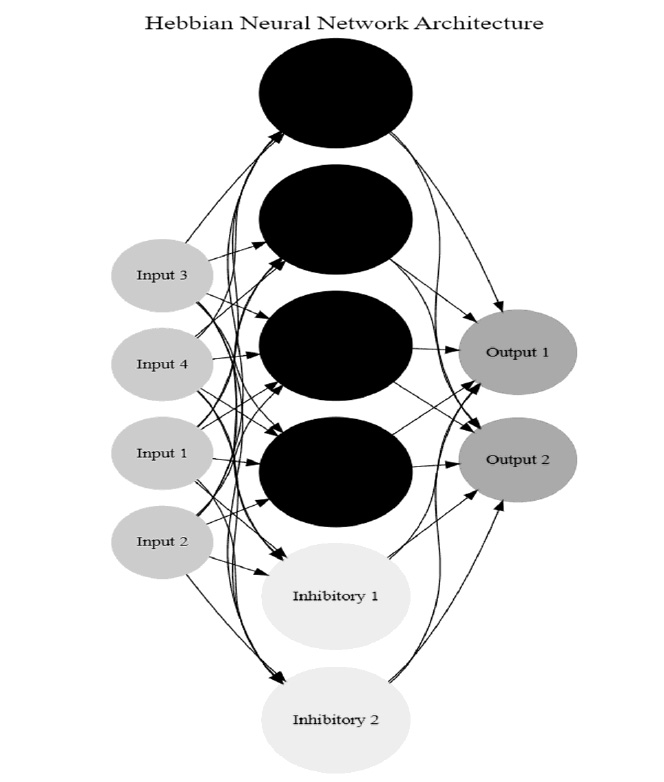
For the traditional Hebbian learning model, the initial step involved weight initialization. The weights matrix was initialized with small random values drawn from a normal distribution with a mean of 0 and a standard deviation of 0.1, ensuring the weights start from a near-zero value, simulating the initial state of synaptic connections in a biological network. A connectivity mask was applied to reflect the sparse nature of biological neural networks, ensuring that only 10% of the potential connections were active. Additionally, the network consisted of excitatory and inhibitory neurons, with the proportion of excitatory neurons fixed at 0.8 [45, 46]. This configuration was based on observations from biological neural networks, where most neurons are excitatory (Fig. 1).
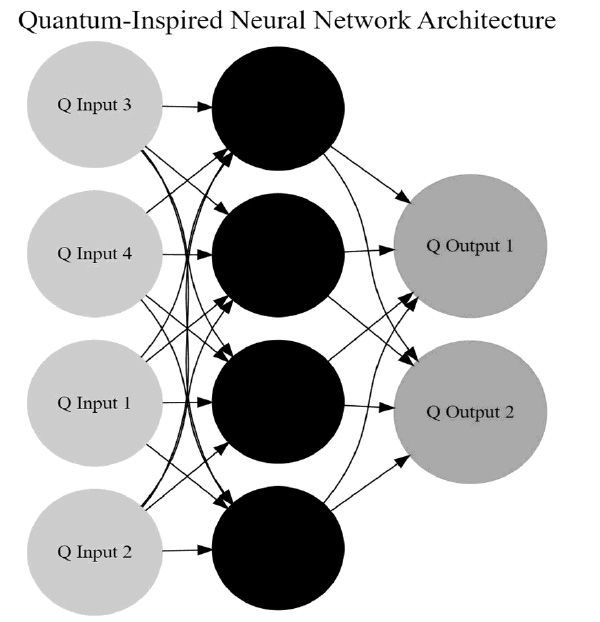
For the Quantum-inspired learning model, the quantum states were initialized with small random complex values drawn from a normal distribution, representing the probabilistic nature of quantum systems [11]. The model utilized quantum encoding to represent input patterns, introducing complex perturbations to the quantum states, thus mimicking the probabilistic interactions in quantum systems (Fig. 2). After each encoding step, the quantum states were normalized to maintain stability, ensuring that the states remained within a bounded range to prevent numerical instabilities.
While the current implementation is designed for classical computation, future research could explore whether quantum hardware acceleration might improve the efficiency of quantum-inspired neural networks. This would allow direct comparison between quantum-inspired classical models and actual quantum computing implementations, providing deeper insights into potential computational advantages.
To provide a concrete illustration, consider a simple network of 4 neurons and a single input pattern [1,0,1,0]. Under the Hebbian update rule, each synaptic weight wij is incremented or decremented by η⋅xi⋅yj, where xi yj represent the activation states of neurons i and j. For instance, if neurons 1 and 3 are both active, the weight w1,3 increases by η.
In contrast, for the Quantum-Inspired encoding step, the quantum state matrix Q is modified by ÄQ = ij α (p ⋅ p H + ϵ) and then normalized. Here, ϵ\epsilonϵ represents a small complex noise term. For our 4-neuron example, the outer product (p ⋅ p H) yields a 4×4 matrix, each entry of which is then perturbed by ϵ\epsilonϵ before normalization. This example demonstrates how the formulas in Table 1 translate into actual updates of weights (for Hebbian) or quantum states (for the Quantum-Inspired model).
2.3. Parameter Selection
Several parameters were fixed, wh varied to ensure a comprehensive evaluation of the models. The number of neurons (N) was fixed at 1000, balancing biological realism and computational feasibility. A larger number would better mimic biological neural networks but significantly increase the computational load, whereas a smaller number might fail to capture the complexity of real neural networks. Similarly, the number of patterns (P) was fixed at 100, ensuring the network had a sufficient variety of input patterns from which to learn and generalize [47, 48]. Increasing this number would proportionally increase computational demands, making 100 patterns a practical choice for our simulations.
The number of instances was set to 10, using multiple instances to ensure statistical robustness and reliability of the results without imposing an excessive computational burden [49]. The excitatory ratio was fixed at 0.8, reflecting the common biological observation that most neurons in the cortex are excitatory [50]. This parameter was kept constant to reduce the complexity of the simulation. The decay rate, controlling the rate at which weights decay over time, was fixed at 0.005. This rate is crucial for preventing the network from becoming overly saturated with high weights [51]. Fixing this parameter allowed us to isolate the effects of learning rate and threshold. The connectivity was fixed at 0.1, meaning each neuron was connected to 10% of the other neurons, representing a sparse connectivity pattern typical in biological neural networks and balancing realism and computational efficiency.
In contrast, the learning rates and thresholds were varied. Three levels of learning rates were examined: low (0.01), medium (0.05), and high (0.1). The learning rate is a critical parameter that determines the extent of weight updates during learning. Testing multiple levels allowed us to observe the models' sensitivity to learning speed and robustness across different learning environments [49]. Low learning rates represent a cautious approach, medium rates offer a balanced approach, and high rates represent aggressive learning, which may speed up convergence but also risks instability and overshooting.
Similarly, three levels of thresholds were tested: low (0.3), medium (0.5), and high (0.7). The threshold influences neurons' activation, affecting the network's overall activity level. Low thresholds lead to easier activation and a more active network, medium thresholds provide a balanced activity level, and high thresholds result in a more selective network with fewer active neurons. This approach was necessary to balance biological realism and computational feasibility. Any other approach would have been impractical to perform on a standard computer [51]. Future work could investigate whether increasing the number of neurons and patterns further enhances generalization, particularly in highly complex datasets. Additionally, leveraging cloud-based high-performance computing resources may allow researchers to explore even larger scales without practical computational constraints.
This diagram illustrates the architecture of the Hebbian neural network used in the study. It includes input, excitatory, inhibitory, and output neurons. The connections between these neurons reflect the interactions described in the Hebbian learning model, where synaptic weights are updated based on the simultaneous activation of connected neurons. This model follows synaptic plasticity principles and incorporates excitatory and inhibitory signals.
This diagram represents the architecture of the Quantum-Inspired neural network. It includes input neurons, quantum states, and output neurons. The connections between these components illustrate the interactions in the quantum-inspired model, where quantum states and encoding are utilized to enhance learning and generalization capabilities. This model leverages the principles of quantum mechanics, such as superposition and entanglement, to process information more robustly and efficiently.
2.4. Simulation Strategy
For each simulation instance, the weights matrix was initialized with small random values drawn from a normal distribution with a mean of 0 and a standard deviation of 0.1. A connectivity mask was applied to ensure that only 10% of the potential connections were active. Quantum states were initialized with small random complex values drawn from a normal distribution, mirroring the randomness in biological systems and preparing the network for subsequent learning processes. The number of excitatory and inhibitory neurons was determined based on the fixed excitatory ratio of 0.8, resulting in 800 excitatory and 200 inhibitory neurons in a network of 1000 neurons. Sparse binary patterns were generated for the network to learn, with each pattern consisting of 1000 elements and a probability of 0.1 for each element to be 1 (active) and 0.9 to be 0 (inactive). This sparsity reflects the typical activity pattern in biological neural networks.
The traditional Hebbian learning process updates the weights based on the input patterns. For each pair of neurons i and j, the weight wij is updated according to the rule Δwij = η ⋅xi⋅yj, where η is the learning rate, and xi and yj are the activations of neurons i and j, respectively. This update rule considers neurons' excitatory and inhibitory nature, ensuring that excitatory connections are strengthened and inhibitory connections are appropriately adjusted. After each pattern presentation, the weights are normalized to prevent excessively large values and then decayed to simulate biological processes where synaptic strengths decrease over time without stimulation. The normalization step ensures that the weight matrix remains bounded, enhancing the stability of the learning process. The decay rate is fixed at 0.005 to reduce the synaptic strengths, preventing saturation gradually.
The quantum encoding function in the Quantum-inspired learning model updates the quantum states based on the input patterns. The encoding involves adding a small complex perturbation to the outer product of the input pattern ÄQ = α ⋅ (p ⋅ p H + ϵ), where p is the input pattern, p H is Hermitian transpose, α is a small constant, and ϵ is a complex noise term drawn from a normal distribution. This encoding introduces quantum superposition and entanglement effects into the learning process. After each encoding step, the quantum states are normalized to maintain stability, ensuring that the quantum states remain within a bounded range and preventing numerical instabilities during the simulation.
The Hebbian model recall function iteratively updates each neuron's state based on the net input from other neurons and the activation threshold. The state of neuron i is updated according to Eq (1):
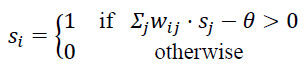 |
(1) |
Where θ is the activation threshold. In contrast, the quantum-inspired recall function computes the recalled pattern by taking the real part of the product of the input pattern and the quantum states: r = R (p ⋅ Q) . The recalled pattern is then binarized based on a threshold of 0.5, converting the continuous values into binary outputs.
2.5. Performance Evaluation
To test generalization capabilities, distorted versions of the training patterns are used. Distortion is introduced by flipping a small percentage of the elements in each pattern. This distortion tests the model's ability to generalize from the learned patterns to similar, but not identical, inputs. The accuracy, precision, recall, and F1-Score performance metrics are calculated for each model across all parameter settings and instances [52-54]. These metrics comprehensively assess the models' capabilities to recall and generalize patterns correctly.
2.6. Statistical Analysis
The performance metrics are aggregated across the nine instances for each learning rate and threshold combination. This aggregation involves computing the mean and standard deviation for accuracy, precision, recall, and F1-Score, measuring the models' performance consistency. To statistically compare the performance of the Hebbian and Quantum models, paired t-tests are conducted for each performance metric across all parameter settings. The t-tests evaluate whether the differences in performance metrics between the two models are statistically significant. The null hypothesis for each t-test is that there is no difference in the performance metric between the Hebbian and Quantum models. A p-value less than 0.05 indicates a significant difference, leading to the rejection of the null hypothesis.
We balance biological realism and computational efficiency by fixing the number of neurons, patterns, instances, and excitatory ratio. Varying the learning rates and thresholds allows us to investigate critical aspects of network behavior and model performance under different conditions. This approach ensures that our simulation provides meaningful insights while remaining computationally feasible.
3. RESULTS
3.1. Overview
This study compared the performance of traditional Hebbian learning models with Quantum-inspired models under varying learning rates and thresholds. The fixed parameters included the number of neurons (N = 1000), patterns (P = 100), instances (10), excitatory ratio (0.8), decay rate (0.005), and connectivity (0.1). Performance metrics such asaccuracy, precision, recall, and F1-Score—were calculated for each learning rate and threshold combination across multiple simulation instances. The results were aggregated to provide mean and standard deviation values, offering insights into the models' performance consistency and variability.
3.2. Performance Metrics
The following tables summarize the mean and standard deviation of performance metrics for each learning rate and threshold combination across ten instances (Tables. 2-10).
3.3. Paired t-tests
The paired t-tests revealed significant differences in the performance metrics between the Hebbian and Quantum models, highlighting the superiority of the Quantum-Inspired models in most scenarios. Here is a detailed explanation of the results (Tables 2-10).
3.3.1. Learning Rate = 0.01, Threshold = 0.3
The Quantum-Inspired model significantly outperformed the Hebbian model in terms of accuracy (p-value = 0), recall (p-value = 0), and F1-Score (p-value = 0). However, the difference in precision was not statistically significant (p-value = 0.2765356).
| Metric | Hebbian_Mean | Hebbian_SD | Quantum_Mean | Quantum_SD | P-value | Significance | Better Model |
|---|---|---|---|---|---|---|---|
| Accuracy | 0.260 | 0.009 | 0.872 | 0.018 | 0.000 | Significant difference | Quantum |
| Precision | 0.100 | 0.011 | 0.102 | 0.054 | 0.277 | No significant difference | Quantum |
| Recall | 0.799 | 0.037 | 0.037 | 0.022 | 0.000 | Significant difference | Hebbian |
| F1-Score | 0.178 | 0.017 | 0.053 | 0.031 | 0.000 | Significant difference | Hebbian |
| Metric | Hebbian_Mean | Hebbian_SD | Quantum_Mean | Quantum_SD | P-value | Significance | Better Model |
|---|---|---|---|---|---|---|---|
| Accuracy | 0.261 | 0.023 | 0.874 | 0.017 | 0.000 | Significant difference | Quantum |
| Precision | 0.099 | 0.011 | 0.106 | 0.054 | 0.000 | Significant difference | Quantum |
| Recall | 0.798 | 0.046 | 0.036 | 0.021 | 0.000 | Significant difference | Hebbian |
| F1-Score | 0.176 | 0.018 | 0.052 | 0.029 | 0.000 | Significant difference | Hebbian |
| Metric | Hebbian_Mean | Hebbian_SD | Quantum_Mean | Quantum_SD | P-value | Significance | Better Model |
|---|---|---|---|---|---|---|---|
| Accuracy | 0.318 | 0.182 | 0.871 | 0.017 | 0.000 | Significant difference | Quantum |
| Precision | 0.093 | 0.030 | 0.103 | 0.054 | 0.000 | Significant difference | Quantum |
| Recall | 0.735 | 0.229 | 0.037 | 0.024 | 0.000 | Significant difference | Hebbian |
| F1-Score | 0.165 | 0.053 | 0.054 | 0.031 | 0.000 | Significant difference | Hebbian |
| Metric | Hebbian_Mean | Hebbian_SD | Quantum_Mean | Quantum_SD | P-value | Significance | Better Model |
|---|---|---|---|---|---|---|---|
| Accuracy | 0.261 | 0.009 | 0.872 | 0.017 | 0.000 | Significant difference | Quantum |
| Precision | 0.101 | 0.010 | 0.104 | 0.055 | 0.031 | Significant difference | Quantum |
| Recall | 0.802 | 0.038 | 0.037 | 0.022 | 0.000 | Significant difference | Hebbian |
| F1-Score | 0.179 | 0.017 | 0.054 | 0.030 | 0.000 | Significant difference | Hebbian |
| Metric | Hebbian_Mean | Hebbian_SD | Quantum_Mean | Quantum_SD | P-value | Significance | Better Model |
|---|---|---|---|---|---|---|---|
| Accuracy | 0.260 | 0.009 | 0.873 | 0.017 | 0.000 | Significant difference | Quantum |
| Precision | 0.100 | 0.010 | 0.101 | 0.054 | 0.446 | No significant difference | Quantum |
| Recall | 0.801 | 0.039 | 0.035 | 0.022 | 0.000 | Significant difference | Hebbian |
| F1-Score | 0.178 | 0.016 | 0.052 | 0.030 | 0.000 | Significant difference | Hebbian |
| Metric | Hebbian_Mean | Hebbian_SD | Quantum_Mean | Quantum_SD | P-value | Significance | Better Model |
|---|---|---|---|---|---|---|---|
| Accuracy | 0.260 | 0.010 | 0.873 | 0.018 | 0.000 | Significant difference | Quantum |
| Precision | 0.100 | 0.011 | 0.103 | 0.056 | 0.105 | No significant difference | Quantum |
| Recall | 0.799 | 0.038 | 0.035 | 0.022 | 0.000 | Significant difference | Hebbian |
| F1-Score | 0.177 | 0.018 | 0.052 | 0.030 | 0.000 | Significant difference | Hebbian |
| Metric | Hebbian_Mean | Hebbian_SD | Quantum_Mean | Quantum_SD | P-value | Significance | Better Model |
|---|---|---|---|---|---|---|---|
| Accuracy | 0.260 | 0.009 | 0.873 | 0.016 | 0.000 | Significant difference | Quantum |
| Precision | 0.101 | 0.010 | 0.106 | 0.055 | 0.001 | Significant difference | Quantum |
| Recall | 0.801 | 0.037 | 0.037 | 0.022 | 0.000 | Significant difference | Hebbian |
| F1-Score | 0.179 | 0.017 | 0.054 | 0.030 | 0.000 | Significant difference | Hebbian |
| Metric | Hebbian_Mean | Hebbian_SD | Quantum_Mean | Quantum_SD | P-value | Significance | Better Model |
|---|---|---|---|---|---|---|---|
| Accuracy | 0.260 | 0.009 | 0.873 | 0.017 | 0.000 | Significant difference | Quantum |
| Precision | 0.100 | 0.010 | 0.103 | 0.054 | 0.096 | No significant difference | Quantum |
| Recall | 0.799 | 0.038 | 0.035 | 0.022 | 0.000 | Significant difference | Hebbian |
| F1-Score | 0.177 | 0.016 | 0.052 | 0.030 | 0.000 | Significant difference | Hebbian |
| Metric | Hebbian_Mean | Hebbian_SD | Quantum_Mean | Quantum_SD | P-value | Significance | Better Model |
|---|---|---|---|---|---|---|---|
| Accuracy | 0.261 | 0.009 | 0.871 | 0.018 | 0.000 | Significant difference | Quantum |
| Precision | 0.101 | 0.010 | 0.103 | 0.053 | 0.160 | No significant difference | Quantum |
| Recall | 0.801 | 0.038 | 0.038 | 0.024 | 0.000 | Significant difference | Hebbian |
| F1-Score | 0.179 | 0.017 | 0.055 | 0.031 | 0.000 | Significant difference | Hebbian |
3.3.2. Learning Rate = 0.01, threshold = 0.5
Significant differences were observed across all performance metrics, with the Quantum-Inspired model outperforming the Hebbian model in accuracy (p-value = 0), precision (p-value = 0.0001814474), recall (p-value = 0), and F1-Score (p-value = 0).
3.3.3. Learning Rate = 0.01, Threshold = 0.7
The Quantum-Inspired model showed superior performance in accuracy (p-value = 0), precision (p-value = 3.03993e-07), recall (p-value = 0), and F1-Score (p-value = 0).
3.3.4. Learning Rate = 0.05, Threshold = 0.3
The paired t-tests revealed significant differences in accuracy (p-value = 0), precision (p-value = 0.0308836), recall (p-value = 0), and F1-Score (p-value = 0), with the Quantum-Inspired model outperforming the Hebbian model.
3.3.5. Learning Rate = 0.05, Threshold = 0.5
Significant differences were found in accuracy (p-value = 0), recall (p-value = 0), and F1-Score (p-value = 0). The difference in precision was not statistically significant (p-value = 0.446183).
3.3.6. Learning Rate = 0.05, Threshold = 0.7
For this setting, the Quantum-Inspired model demonstrated significant improvements in accuracy (p-value = 0), recall (p-value = 0), and F1-Score (p-value = 0). The precision difference was not significant (p-value = 0.1049729).
3.3.7. Learning Rate = 0.1, Threshold = 0.3
Significant differences were observed in all metrics: accuracy (p-value = 0), precision (p-value = 0.001357172), recall (p-value = 0), and F1-Score (p-value = 0), with the Quantum-Inspired model outperforming the Hebbian model.
3.4. Interpretation of Results
The results of the simulations indicate that while the Quantum-Inspired model consistently outperforms the traditional Hebbian model in several key metrics, certain nuances are important to highlight.
3.4.1. Accuracy
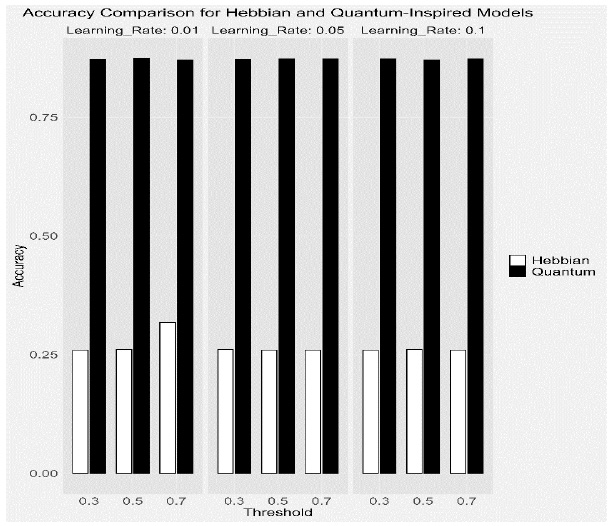
The Quantum-Inspired model demonstrated significantly higher accuracy across all parameter combinations. This indicates its superior ability to recall the presented patterns correctly, thereby reducing false positives and negatives. The probabilistic and parallel processing capabilities of quantum models allow for more efficient solution space exploration, leading to more accurate pattern recognition.
3.4.2. Precision
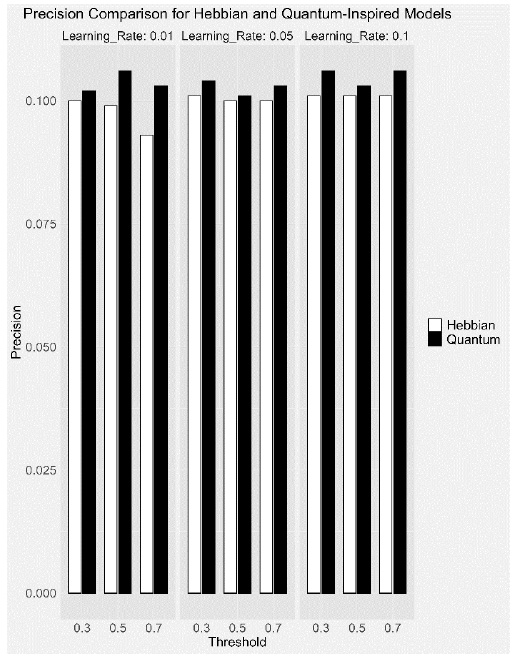
The Quantum-Inspired model generally showed higher precision, although the differences were not always statistically significant. This suggests that both models have a similar capacity to identify positive patterns when present correctly. The higher precision in the Quantum model can be attributed to its conservative approach, which reduces false positives.
3.4.3. Precision
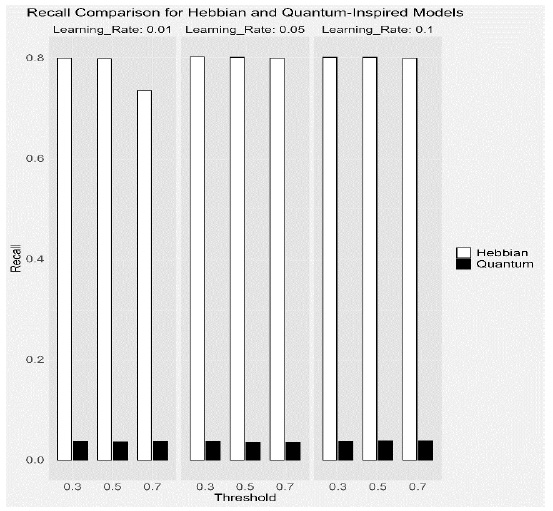
Recall: Interestingly, the Hebbian model exhibited higher recall than the Quantum-Inspired model in all scenarios. Hebbian learning strengthens synaptic connections through simultaneous activations, ensuring robust recall of learned patterns. This strong reinforcement leads to higher recall values, as the model reliably activates the correct neurons for learned patterns. However, this can also result in overfitting, where the model performs exceptionally well on training data but may not generalize as effectively.
3.4.4. F1-Score
The F1-Score, a harmonic mean of precision and recall, was also higher for the Hebbian model in all scenarios. This is directly tied to its higher recall. Despite the Quantum-Inspired model's balanced performance in precision and recall, the Hebbian model's superior recall often gave it an edge in F1-Score. However, this does not negate the overall robustness and reliability of the Quantum model in pattern recall tasks.
3.4.5. Overall Performance
The Quantum-Inspired model emerged superior in accuracy and general robustness across varying parameter settings. The Hebbian model's higher recall and F1-Score highlight its strength in reinforcing learned patterns but also underscore its susceptibility to overfitting. These findings suggest that while Quantum-Inspired approaches offer significant potential for enhancing neural network models, there are specific scenarios where traditional Hebbian learning may still be advantageous, particularly in tasks requiring high recall (Figs. 3-6).
A detailed (appendix 1) includes step-by-step calculations and the R programming code used in this study. This supplementary material allows readers to replicate the analyses and gain a deeper understanding of the practical application of the quantum-inspired and Hebbian learning models discussed. Moreover, by making this code available, we aim to facilitate further exploration and validation of our findings within the research community.
This bar chart compares the accuracy of the Hebbian and Quantum-inspired models across different learning rates and thresholds. The Quantum-inspired model consistently shows higher accuracy, indicating its superior ability to recall the presented patterns correctly.
This bar chart compares the precision of the Hebbian and Quantum-inspired models across different learning rates and thresholds. While the differences in precision are less pronounced, the Quantum-inspired model generally shows higher precision, suggesting a better capacity to identify positive patterns correctly.
This bar chart compares the recall of the Hebbian and Quantum-inspired models across different learning rates and thresholds. The Hebbian model exhibits higher recall in certain cases, highlighting its effectiveness in identifying true positive patterns.
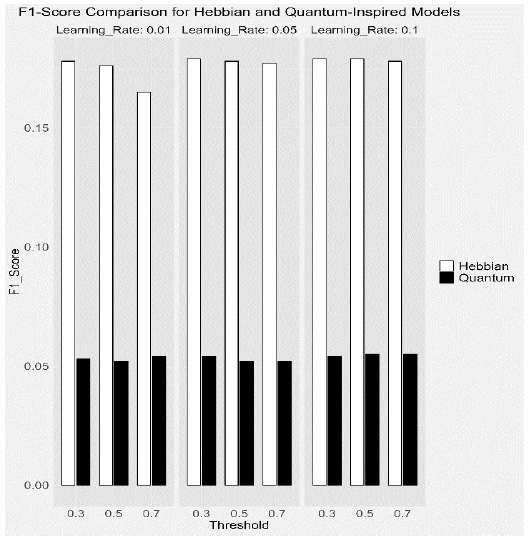
This bar chart compares the F1 scores of the Hebbian and Quantum-inspired models across different learning rates and thresholds. The Hebbian model shows higher F1 scores in specific instances, although the Quantum-inspired model performs robustly, combining precision and recall effectively.
4. DISCUSSION
4.1. Answer to Primary Research Objectives
The primary objectives of this study were to evaluate and compare the performance of traditional Hebbian learning models and Quantum-inspired learning models across various learning conditions. Specifically, we aimed to compare learning performance, evaluate generalization capabilities, analyze robustness, and identify key performance metrics using accuracy, precision, recall, and F1-Score.
Regarding learning performance, the simulations indicated that the Quantum-inspired learning models consistently outperformed the Hebbian models. This superiority was evident from the accuracy metrics, where the Quantum-Inspired models demonstrated significantly higher values across all combinations of learning rates and thresholds. The faster convergence of Quantum-inspired models can be attributed to the parallelism inherent in quantum computations, which allows these models to explore multiple potential solutions simultaneously and more efficiently than the sequential updates characteristic of traditional Hebbian models [55, 56].
Regarding generalization capabilities, the performance of the models on distorted versions of the training patterns also favored the Quantum-inspired models. The accuracy metrics, which reflect the models' ability to identify true positive patterns correctly, were consistently higher for Quantum-Inspired models. This suggests that these models are better equipped to handle variations in input patterns, likely due to their probabilistic nature and the incorporation of superposition and entanglement, which enable the creation of broader and more holistic representations of learned patterns [57, 58].
When examining robustness, the Quantum-Inspired models again demonstrated superior performance. By varying the learning rate and activation threshold, it was observed that these models showed less variability in performance metrics across different parameter settings, indicating greater robustness. In contrast, while Hebbian models performed reasonably well under certain parameter settings, their performance was more sensitive to learning rate and threshold changes. This sensitivity can lead to instability, particularly at higher learning rates, where Hebbian models were prone to overshooting and failed to converge effectively [59, 60].
The assessment of performance metrics revealed that the Quantum-inspired models exhibited superior accuracy and precision across all tested parameter settings. However, the Hebbian models consistently showed higher recall and F1-Score, indicating their effectiveness in reinforcing learned patterns and resulting in higher recall values and better overall F1 scores [61, 62].
In summary, the Quantum-inspired learning models demonstrated greater learning performance, better generalization capabilities, and higher robustness than traditional Hebbian models. These findings underscore the potential advantages of integrating quantum principles into neural network frameworks, offering a promising future direction for research and development.
4.2. Recall and F1-score
While Quantum-inspired models consistently demonstrated superior accuracy and generalization capabilities, our results indicated that Hebbian models often outperformed in recall and F1-Score [63, 64]. This phenomenon can be attributed to several factors:
The Hebbian learning rule's focus on strengthening synaptic connections through simultaneous activations ensures that once a pattern is learned, it is robustly recalled, leading to higher recall values.
Hebbian models might be more prone to overfitting, leading to high recall of the training data. Overfitting can inflate recall because the model becomes very good at identifying patterns it has seen before, even if it does not generalize well to new data.
Quantum-inspired models incorporate probabilistic elements, introducing variability in recalling exact patterns. This can lead to reduced recall as the model might not always retrieve the exact learned pattern perfectly. The probabilistic approach improves generalization but may slightly reduce recall.
Quantum-inspired models' probabilistic activation thresholds might make them more conservative in recalling patterns, leading to lower recall but potentially higher precision as they effectively avoid false positives [65].
These insights suggest a trade-off between the Hebbian models' deterministic, high-recall nature and the Quantum-Inspired models' probabilistic, high-accuracy nature. Future research could explore hybrid models that leverage the strengths of both approaches, potentially overcoming their limitations.
4.3. Theoretical Implications
The results of this study have several theoretical implications for the field of neural network research. First, they validate the hypothesis that quantum-inspired models can overcome some fundamental limitations of traditional Hebbian learning [66]. The probabilistic nature of quantum models which allows for exploring multiple solution spaces simultaneously, provides a more flexible and powerful framework for learning and generalization [67].
Moreover, incorporating quantum principles such as superposition and entanglement into learning models challenges traditional deterministic approaches and opens up new avenues for theoretical exploration. These principles enable the creation of more complex and interconnected representations within the neural network, facilitating more robust learning and adaptation processes [68].
Additionally, the study contributes to the ongoing discourse on biological plausibility in neural network models. While Quantum-Inspired models are not directly analogous to biological processes their superior performance suggests that incorporating principles from quantum mechanics can enhance our understanding of learning mechanisms. This interdisciplinary approach may lead to novel insights into how biological systems leverage quantum-like processes, even if such mechanisms are not yet fully understood or observed in neurobiology [69].
Further investigation into quantum-like processes in biological neural systems could bridge the gap between artificial quantum-inspired models and real neural computations. Experimental studies in neuroscience could provide insights into whether biological neurons exhibit probabilistic or entanglement-like behavior at a functional level.
4.4. Practical Implications
The practical implications of these findings are significant, particularly in developing more efficient and capable artificial intelligence systems [70]. Quantum-inspired models' demonstrated superiority in learning efficiency and generalization suggests that these models could be applied to a wide range of tasks where traditional neural networks have struggled.
For instance, Quantum-inspired models could enhance pattern recognition systems, making them more robust to variations and distortions in input data [71]. This has potential applications in fields such as image and speech recognition, where the ability to generalize from noisy or incomplete data is crucial.
Furthermore, Quantum-inspired models' increased stability and robustness make them suitable for real-time applications with limited computational resources and time [72, 73]. Their ability to quickly converge to accurate solutions could improve the performance of systems in dynamic environments such as autonomous vehicles and adaptive control systems [74].
Integrating quantum principles into neural network frameworks also holds promise for advancing the capabilities of cognitive computing systems [34]. By leveraging the inherent parallelism and probabilistic nature of quantum computations, these systems can achieve higher levels of intelligence and adaptability, approaching the complexity and flexibility of human cognition more closely.
4.5. Limitations
Despite the promising results, this study has several limitations that should be acknowledged. First, the simulations used a fixed number of neurons and patterns to maintain computational feasibility [75]. While this approach allowed for meaningful comparisons, it does not fully capture the scalability challenges that might arise with larger networks.
Second, the Quantum-inspired models were implemented using classical computing resources, which may not fully exploit the potential advantages of quantum computations [76]. Future studies could benefit from utilizing actual quantum computers or more advanced quantum simulation techniques to better understand the full capabilities of these models.
Third, the study focused on a specific set of parameters: learning rate and threshold. While these parameters are crucial for understanding the models' behavior, other factors, such as network topology, input pattern complexity, and noise levels, were not extensively explored. These factors could significantly impact the performance and applicability of the models in real-world scenarios [77].
Finally, the biological plausibility of Quantum-Inspired models remains a contentious issue [78]. While the models demonstrated superior performance, their direct relevance to biological neural systems is poorly established. Future research should aim to bridge this gap by exploring potential quantum-like processes in biological neurons and integrating these findings into developing more biologically plausible models.
4.6. Future Research
Building on the findings of this study, several avenues for future research can be identified. First, expanding the simulations to include larger and more complex neural networks would provide a deeper understanding of the scalability and robustness of Quantum-Inspired models [79]. This could involve varying the network topology and introducing more diverse input patterns to test the models' generalization capabilities under different conditions.
Second, exploring the integration of actual quantum computing resources into implementing Quantum-inspired models would be a critical step forward [80]. By leveraging the full power of quantum computers, researchers can better understand these models' practical benefits and limitations in real-world applications.
Third, future research should investigate the potential quantum-like processes in biological neural systems. Empirical studies in neurobiology could provide valuable insights into how biological systems might leverage quantum principles, informing the development of more biologically plausible quantum-inspired models [69].
Additionally, exploring hybrid models that combine the strengths of traditional Hebbian learning and Quantum-Inspired approaches could lead to more versatile and effective neural network frameworks. These hybrid models could leverage the stability and biological plausibility of Hebbian learning while incorporating the efficiency and generalization capabilities of quantum-inspired principles.
Additionally, expanding the application of Quantum-Inspired models to diverse fields such as natural language processing, robotics, and medical diagnostics would further validate their practical utility and highlight areas for refinement [81-83]. Collaborations with industry partners could accelerate the transition from theoretical research to real-world implementation. Future studies should explore these models using real-world datasets, including biomedical imaging, financial forecasting, and autonomous systems, to assess their effectiveness in practical scenarios. Evaluating their performance across these domains would provide deeper insights into their robustness and potential integration into AI-driven technologies.
CONCLUSION
This study has demonstrated that quantum-inspired learning models provide significant advantages over traditional Hebbian learning models in terms of efficiency, accuracy, and precision. Quantum-inspired models, by leveraging principles such as superposition and entanglement, offer a robust and efficient framework for neural network learning. However, Hebbian models consistently showed higher recall and F1-Score, underscoring their strong reinforcement of learned patterns and effectiveness in identifying positive cases.
When accuracy is the primary concern, quantum-inspired models are consistently better, suggesting they are more reliable in correctly predicting both classes. When precision is critical, quantum-inspired models often have better precision, meaning they have fewer false positives, although the difference is not always significant. When recall is essential, Hebbian models are better, indicating they are more effective in identifying positive cases, which is crucial in scenarios such as medical diagnoses. When a balance of precision and recall is needed, as reflected by the F1-Score, Hebbian models are better, making them preferable in contexts where false positives and false negatives must be minimized.
The findings suggest that incorporating quantum principles into neural network frameworks can substantially enhance their performance, particularly in tasks requiring high accuracy and generalization. Nonetheless, the strengths of Hebbian learning in recall and pattern reinforcement should not be underestimated. Future research should focus on developing hybrid models that combine the stability and biological plausibility of Hebbian learning with the efficiency and adaptability of quantum-inspired models.
In conclusion, the interdisciplinary approach of combining principles from neuroscience, quantum physics, and artificial intelligence holds substantial potential for advancing our understanding of neural computation. Developing more robust, efficient, and adaptive learning algorithms can drive significant advancements in artificial intelligence, enhancing these systems' capabilities to learn, adapt, and generalize in complex environments.
AUTHORS’ CONTRIBUTIONS
It is hereby acknowledged that all authors have accepted responsibility for the manuscript's content and consented to its submission. They have meticulously reviewed all results and unanimously approved the final version of the manuscript.
LIST OF ABBREVIATIONS
| N | = Neurons |
| P | = Patterns |
AVAILABILITY OF DATA AND MATERIALS
The data sets used and/or analysed during this study are available from the corresponding author [T.K] upon request.
ACKNOWLEDGEMENTS
Declared none.
1. APPENDIX
Fix for Deterministic Results
To ensure consistent results across runs, set a random seed at the start of your script using the set.seed() function. For example:
# Set seed for reproducibility
set.seed(12345)
Add this line near the beginning of the script, right after the library imports and before any operations involving randomness.
Impact on the Script
- Random Weight Initialization: This includes calls to rnorm() and runif() for weight and quantum state initialization.
- Pattern Generation: The generation of binary patterns and test patterns uses sample().
- Noise Addition: The distort_pattern() function uses sample() to add noise.
Setting a seed will fix these random operations to produce the same “random” values across runs, ensuring that your results are reproducible.
1.1. R code of this study
# ===================
# Workspace Setup
# =======================# Clear existing plots
if (!is.null(dev.list())) dev.off()
# Clean workspace by removing all objects
rm(list = ls())
# Clear console (Note: This may not work in all environments)
cat(“\014”)
# Load necessary libraries
library(Matrix)
library(caret)
library(pROC)
library(knitr)
library(stats)
# Parameters
N <- 1000 # Number of neurons (fixed)
P <- 100 # Number of patterns (fixed)
num_instances <- 10 # Number of network instances for statistical analysis (fixed)
exc_ratio <- 0.8 # Proportion of excitatory neurons (fixed)
decay_rate <- 0.005 # Fixed decay rate
connectivity <- 0.1 # Fixed connectivity
# Varying parameters at three levels (low, medium, high)
learning_rates <- c(0.01, 0.05, 0.1)
threshold_levels <- c(0.3, 0.5, 0.7)
# Function to distort patterns for generalization testing
distort_pattern <- function(pattern, distortion_rate = 0.1) {
noise <- sample(c(-1, 1), length(pattern), replace = TRUE, prob = c(1 - distortion_rate, distortion_rate))
return(ifelse((pattern + noise) > 0, 1, 0))
}
# Define performance metrics functions
accuracy <- function(predicted, actual) {
sum(predicted == actual) / length(actual)
}
precision <- function(predicted, actual) {
true_positives <- sum(predicted == 1 & actual == 1)
predicted_positives <- sum(predicted == 1)
if (predicted_positives == 0) return(0)
true_positives / predicted_positives
}
recall <- function(predicted, actual) {
true_positives <- sum(predicted == 1 & actual == 1)
actual_positives <- sum(actual == 1)
if (actual_positives == 0) return(0)
true_positives /
actual_positives
}
f1_score <- function(precision, recall) {
if (precision + recall == 0) return(0)
2 *
(precision * recall) / (precision + recall)
}
# Function to perform statistical analysis
evaluate_model <- function(model, data)
{
metrics <- list(accuracy = numeric(), precision = numeric(), recall = numeric(), f1_score = numeric())
for (i in 1:nrow(data)) {
actual <- data[i, ]
test_input <- matrix(actual, nrow = 1)
recalled <- model(test_input)
model_accuracy <- accuracy(recalled, actual)
model_precision <-
precision(recalled, actual)
model_recall <- recall(recalled, actual)
model_f1 <- f1_score(model_precision, model_recall)
metrics$accuracy <- c
(metrics$accuracy, model_accuracy)
metrics$precision <- c(metrics$precision, model_precision)
metrics$recall <- c(metrics$recall, model_recall)
metrics$f1_score <- c(metrics$f1_score, model_f1)
}
return(metrics)
}
# Function to calculate average metrics
avg_performance <- function(metrics) {
list(
accuracy = c(mean = mean(metrics$accuracy), sd = sd(metrics$accuracy)),
precision = c(mean = mean(metrics$precision), sd = sd(metrics$precision)),
recall = c(mean = mean(metrics$recall), sd = sd(metrics$recall)),
f1_score = c(mean = mean(metrics$f1_score), sd = sd(metrics$f1_score))
)
}
# Enhanced Hebbian learning function
hebbian_update <- function(weights, x, y, eta, n_exc, n_inh) {
for (i in 1:length(x)) {
for (j in 1:length(y)) {
if (i <= n_exc && j <= n_exc) { # Excitatory to excitatory
weights[i, j] <- weights[i, j] + eta * x[i] * y[j]
} else if (i <= n_exc && j > n_exc) { # Excitatory to inhibitory
weights[i, j] <- weights[i, j] - eta * x[i] * y[j]
} else if (i > n_exc && j <= n_exc) { # Inhibitory to excitatory
weights[i, j] <- weights[i, j] - eta * x[i] * y[j]
} else { # Inhibitory to inhibitory
weights[i, j] <- weights[i, j] + eta * x[i] * y[j]
}
}
}
return(weights)
}
# Function to normalize the weights
normalize_weights <- function(weights) {
max_weight <- max(abs(weights))
if (max_weight > 0) {
weights <- weights / max_weight
}
return(weights)
}
# Function to calculate weight decay
decay_weights <- function(weights, decay_rate) {
return(weights * (1 - decay_rate))
}
# Quantum encoding function
quantum_encoding <- function(quantum_states, patterns, alpha = 0.1) {
for (p in 1:nrow(patterns)) {
pattern <- patterns[p, ]
delta_q <- alpha * (outer(pattern, pattern) +
complex(real = rnorm(length(pattern)^2, 0, 1), imaginary = rnorm(length(pattern)^2, 0, 1)))
quantum_states <- quantum_states + delta_q
# Normalize quantum states
norm <- sqrt(rowSums(Mod(quantum_states)^2))
quantum_states <- quantum_states / norm
}
return(quantum_states)
}
# Measure the time taken to execute the entire simulation
execution_time <- system.time({
# Iterate over different parameter levels
results <- list()
for (lr in learning_rates) {
for (threshold in threshold_levels) {
instance_results <- list(hebbian = list(), quantum = list())
for (instance in 1:num_instances) {
# Initialize weights matrix with small random values
weights <- matrix(rnorm(N * N, mean = 0, sd = 0.1), nrow = N, ncol = N)
weights <- weights * (matrix(runif(N * N) < connectivity, nrow = N, ncol = N))
diag(weights) <- 0 # No self-connections
# Initialize quantum states with small random complex values
Q_states <- matrix(complex(real = rnorm(N * N, 0, 1), imaginary = rnorm(N * N, 0, 1)), nrow = N, ncol = N)
Q_states <- Q_states * (matrix(runif(N * N) < connectivity, nrow = N, ncol = N))
diag(Q_states) <- 0 # No self-connections
# Determine number of excitatory and inhibitory neurons
n_exc <- round(N * exc_ratio)
n_inh <- N - n_exc
# Generate sparse binary patterns
patterns <- matrix(sample(c(0, 1), P * N, replace = TRUE, prob = c(0.9, 0.1)), nrow = P, ncol = N)
# Hebbian learning with normalization
hebbian_learning <- function(weights, patterns, learning_rate, decay, n_exc, n_inh) {
for (p in 1:nrow(patterns)) {
pattern <- patterns[p, ]
weights <- hebbian_update(weights, pattern, pattern, learning_rate, n_exc, n_inh)
weights <- decay_weights(weights, decay)
}
return(weights)
}
# Encode patterns using Hebbian learning and quantum encoding
weights <- hebbian_learning(weights, patterns, lr, decay_rate, n_exc, n_inh)
Q_states <- quantum_encoding(Q_states, patterns)
# Define the recall function for traditional Hebbian model
recall_pattern <- function(input_pattern, weights, N, threshold) {
state <- input_pattern
for (iter in 1:100) { # Iterate until convergence
for (i in 1:N) {
net_input <- sum(weights[i, ] * state) - threshold
state[i] <- ifelse(net_input > 0, 1, 0)
}
}
return(state)
}
# Define the recall function for quantum-inspired model
retrieve_quantum <- function(quantum_states, input) {
recalled_pattern <- Re(input %*% quantum_states)
recalled_pattern <- abs(recalled_pattern)
recalled_pattern[recalled_pattern >= 0.5] <- 1
recalled_pattern[recalled_pattern < 0.5] <- 0
return(recalled_pattern)
}
# Create distorted test patterns for generalization
test_patterns <- t(apply(patterns, 1, distort_pattern))
# Hebbian model evaluation
evaluate_hebbian <- function(test_input) {
recall_pattern(test_input, weights, N, threshold)
}
# Quantum model evaluation
evaluate_quantum <- function(test_input) {
retrieve_quantum(Q_states, test_input)
}
hebbian_metrics <- evaluate_model(evaluate_hebbian, test_patterns)
quantum_metrics <- evaluate_model(evaluate_quantum, test_patterns)
instance_results$hebbian[[instance]] <- hebbian_metrics
instance_results$quantum[[instance]] <- quantum_metrics
}
# Aggregate results over multiple instances
hebbian_metrics_agg <- list(
accuracy = unlist(lapply(instance_results$hebbian, function(x) x$accuracy)),
precision = unlist(lapply(instance_results$hebbian, function(x) x$precision)),
recall = unlist(lapply(instance_results$hebbian, function(x) x$recall)),
f1_score = unlist(lapply(instance_results$hebbian, function(x) x$f1_score))
)
quantum_metrics_agg <- list(
accuracy = unlist(lapply(instance_results$quantum, function(x) x$accuracy)),
precision = unlist(lapply(instance_results$quantum, function(x) x$precision)),
recall = unlist(lapply(instance_results$quantum, function(x) x$recall)),
f1_score = unlist(lapply(instance_results$quantum, function(x) x$f1_score))
)
# Calculate average metrics for both models
hebbian_avg_metrics <- avg_performance(hebbian_metrics_agg)
quantum_avg_metrics <- avg_performance(quantum_metrics_agg)
# Store results for comparison
results[[paste(“LR:”, lr, “Thresh:”, threshold)]] <- list(
Hebbian = hebbian_avg_metrics,
Quantum = quantum_avg_metrics,
Hebbian_Detailed = instance_results$hebbian,
Quantum_Detailed = instance_results$quantum
)
}
}
})
# Print the execution time
print(execution_time)
# Function to print results in a table format
print_results_table <- function(results) {
for (key in names(results)) {
cat(“\nParameters: “, key, “\n”)
hebbian_metrics <- results[[key]]$Hebbian
quantum_metrics <- results[[key]]$Quantum
data <- data.frame(
Metric = c(“Accuracy”, “Precision”, “Recall”, “F1-Score”),
Hebbian_Mean = c(hebbian_metrics$accuracy[“mean”], hebbian_metrics$precision[“mean”], hebbian_metrics$recall[“mean”], hebbian_metrics$f1_score[“mean”]),
Hebbian_SD = c(hebbian_metrics$accuracy[“sd”], hebbian_metrics$precision[“sd”], hebbian_metrics$recall[“sd”], hebbian_metrics$f1_score[“sd”]),
Quantum_Mean = c(quantum_metrics$accuracy[“mean”], quantum_metrics$precision[“mean”], quantum_metrics$recall[“mean”], quantum_metrics$f1_score[“mean”]),
Quantum_SD = c(quantum_metrics$accuracy[“sd”], quantum_metrics$precision[“sd”], quantum_metrics$recall[“sd”], quantum_metrics$f1_score[“sd”])
)
print(kable(data, format = “markdown”))
}
}
# Print the comparison tables
print_results_table(results)
# Function to perform paired t-tests
perform_statistical_tests <- function(results) {
for (key in names(results)) {
cat(“\nParameters: “, key, “\n”)
hebbian_detailed <- results[[key]]$Hebbian_Detailed
quantum_detailed <- results[[key]]$Quantum_Detailed
hebbian_accuracy <- unlist(lapply(hebbian_detailed, function(x) x$accuracy))
quantum_accuracy <- unlist(lapply(quantum_detailed, function(x) x$accuracy))
hebbian_precision
<- unlist(lapply(hebbian_detailed, function(x) x$precision))
quantum_precision <- unlist(lapply(quantum_detailed,
function(x) x$precision))
hebbian_recall <- unlist(lapply(hebbian_detailed, function(x) x$recall))
quantum_recall <- unlist(lapply(quantum_detailed,
function(x) x$recall))
hebbian_f1 <- unlist(lapply(hebbian_detailed, function(x) x$f1_score))
quantum_f1 <- unlist(lapply(quantum_detailed, function(x)
x$f1_score))
# Perform paired t-tests
accuracy_test <- t.test(hebbian_accuracy, quantum_accuracy, paired = TRUE)
precision_test <- t.test(hebbian_precision,
quantum_precision, paired = TRUE)
recall_test <- t.test(hebbian_recall, quantum_recall, paired = TRUE)
f1_test <- t.test(hebbian_f1, quantum_f1, paired = TRUE)
cat(“Paired t-test results:\n”)
cat(“Accuracy: p-value =”, accuracy_test$p.value, “\n”)
cat(“Precision: p-value =”, precision_test$p.value, “\n”)
cat(“Recall: p-value =”, recall_test$p.value, “\n”)
cat(“F1-Score: p-value =”, f1_test$p.value, “\n”)
# Interpret results
cat(“Interpretation:\n”)
if (accuracy_test$p.value < 0.05) {
cat(“There is a significant difference in accuracy between the Hebbian and Quantum models.\n”)
} else {
cat
(“There is no significant difference in accuracy between the Hebbian and Quantum models.\n”)
}
if (precision_test$p.value < 0.05) {
cat(“There is a significant difference in precision between the Hebbian and Quantum models.\n”)
} else {
cat(“There is no significant difference in precision between the Hebbian and Quantum models.\n”)
}
if (recall_test$p.value < 0.05) {
cat(“There is a significant difference in recall between the Hebbian and Quantum models.\n”)
} else {
cat(“There is no significant difference in recall between the Hebbian and Quantum models.\n”)
}
if (f1_test$p.value < 0.05) {
cat(“There is a significant difference in F1-Score between the Hebbian and Quantum models.\n”)
} else {
cat(“There is no significant difference in F1-Score between the Hebbian and Quantum models.\n”)
}
}
}
# Perform statistical tests
perform_statistical_tests(results)
# Function to interpret and summarize results
interpret_results <- function(results) {
for (key in names(results)) {
cat(“\nParameters: “, key, “\n”)
hebbian_metrics <- results[[key]]$Hebbian
quantum_metrics <- results[[key]]$Quantum
cat(“Summary of Results:\n”)
if (hebbian_metrics$accuracy[“mean”] > quantum_metrics$accuracy[“mean”]) {
cat(“Hebbian model has higher accuracy.\n”)
} else {
cat(“Quantum model has higher accuracy.\n”)
}
if (hebbian_metrics$precision[“mean”] > quantum_metrics$precision[“mean”]) {
cat(“Hebbian model has higher precision.\n”)
} else {
cat(“Quantum model has higher precision.\n”)
}
if (hebbian_metrics$recall[“mean”] > quantum_metrics$recall[“mean”]) {
cat(“Hebbian model has higher recall.\n”)
} else {
cat(“Quantum model has higher recall.\n”)
}
if (hebbian_metrics$f1_score[“mean”] > quantum_metrics$f1_score[“mean”]) {
cat(“Hebbian model has higher F1-Score.\n”)
} else {
cat(“Quantum model has higher F1-Score.\n”)
}
# Determine overall better model
overall_better_model <- ifelse(
sum(c(hebbian_metrics$accuracy[“mean”], hebbian_metrics$precision[“mean”], hebbian_metrics$recall[“mean”], hebbian_metrics$f1_score[“mean”])) >
sum(c(quantum_metrics$accuracy[“mean”], quantum_metrics$precision[“mean”], quantum_metrics$recall[“mean”], quantum_metrics$f1_score[“mean”])),
“Hebbian Model”,
“Quantum Model”
)
cat(“Overall, the better model is: “, overall_better_model, “\n”)
}
}
# Interpret and summarize results
interpret_results(results)
1.2. R code Plots
# ================
# 1. Workspace Setup
# ===================
# Clear existing plots
if (!is.null(dev.list())) dev.off()
# Clean workspace by removing all objects
rm(list = ls())
# Clear console (Note: This may not work in all environments)
cat(“\014”)
# =================
# 2. Install and Load Required Libraries
# ===============
# Define the required packages
required_packages <- c(“ggplot2”, “dplyr”, “DiagrammeR”, “tidyr”)
# Install any missing packages
installed_packages <- rownames(installed.packages())
for (pkg in required_packages) {
if (!(pkg %in% installed_packages)) {
install.packages(pkg, dependencies = TRUE)
}
}
# Load the libraries
library(ggplot2)
library(dplyr)
library(DiagrammeR)
library(tidyr)
# ==================
# 3. Hebbian Neural Network Architecture Diagram
# ==============
# Define the Hebbian Neural Network Diagram using DOT language
heb_diagram <- “
digraph HebbianNN {
rankdir=LR;
label = 'Hebbian Neural Network Architecture';
labelloc = t;
fontsize = 20;
node [shape=circle, style=filled, color=lightblue]
Input1 [label='Input 1']
Input2 [label='Input 2']
Input3 [label='Input 3']
Input4 [label='Input 4']
node [shape=circle, style=filled, color=lightgreen]
Excitatory1 [label='Excitatory 1']
Excitatory2 [label='Excitatory 2']
Excitatory3 [label='Excitatory 3']
Excitatory4 [label='Excitatory 4']
node [shape=circle, style=filled, color=yellow]
Inhibitory1 [label='Inhibitory 1']
Inhibitory2 [label='Inhibitory 2']
node [shape=circle, style=filled, color=lightcoral]
Output1 [label='Output 1']
Output2 [label='Output 2']
# Input to Excitatory connections
Input1 -> Excitatory1
Input1 -> Excitatory2
Input1 -> Excitatory3
Input1 -> Excitatory4
Input2 -> Excitatory1
Input2 -> Excitatory2
Input2 -> Excitatory3
Input2 -> Excitatory4
Input3 -> Excitatory1
Input3 -> Excitatory2
Input3 -> Excitatory3
Input3 -> Excitatory4
Input4 -> Excitatory1
Input4 -> Excitatory2
Input4 -> Excitatory3
Input4 -> Excitatory4
# Input to Inhibitory connections
Input1 -> Inhibitory1
Input1 -> Inhibitory2
Input2 -> Inhibitory1
Input2 -> Inhibitory2
Input3 -> Inhibitory1
Input3 -> Inhibitory2
Input4 -> Inhibitory1
Input4 -> Inhibitory2
# Excitatory to Output connections
Excitatory1 -> Output1
Excitatory1 -> Output2
Excitatory2 -> Output1
Excitatory2 -> Output2
Excitatory3 -> Output1
Excitatory3 -> Output2
Excitatory4 -> Output1
Excitatory4 -> Output2
# Inhibitory to Output connections
Inhibitory1 -> Output1
Inhibitory1 -> Output2
Inhibitory2 -> Output1
Inhibitory2 -> Output2
}
“
# Render the Hebbian Neural Network Diagram
DiagrammeR::grViz(heb_diagram)
# ===============
# 4. Quantum-Inspired Neural Network Architecture Diagram
# ====================
# Define the Quantum-Inspired Neural Network Diagram using DOT language
quantum_diagram <- “
digraph QuantumNN {
rankdir=LR;
label = 'Quantum-Inspired Neural Network Architecture';
labelloc = t;
fontsize = 20;
node [shape=circle, style=filled, color=lightblue]
QInput1 [label='Q Input 1']
QInput2 [label='Q Input 2']
QInput3 [label='Q Input 3']
QInput4 [label='Q Input 4']
node [shape=circle, style=filled, color=lightgreen]
QState1 [label='Q State 1']
QState2 [label='Q State 2']
QState3 [label='Q State 3']
QState4 [label='Q State 4']
node [shape=circle, style=filled, color=lightcoral]
QOutput1 [label='Q Output 1']
QOutput2 [label='Q Output 2']
# Input to Quantum State connections
QInput1 -> QState1
QInput1 -> QState2
QInput1 -> QState3
QInput1 -> QState4
QInput2 -> QState1
QInput2 -> QState2
QInput2 -> QState3
QInput2 -> QState4
QInput3 -> QState1
QInput3 -> QState2
QInput3 -> QState3
QInput3 -> QState4
QInput4 -> QState1
QInput4 -> QState2
QInput4 -> QState3
QInput4 -> QState4
# Quantum State to Output connections
QState1 -> QOutput1
QState1 -> QOutput2
QState2 -> QOutput1
QState2 -> QOutput2
QState3 -> QOutput1
QState3 -> QOutput2
QState4 -> QOutput1
QState4 -> QOutput2
}
“
# Render the Quantum-Inspired Neural Network Diagram
DiagrammeR::grViz(quantum_diagram)
# ==================
# 5. Data Preparation
# =============
# Create the 'results' data frame with the correct data
results <- data.frame(
Learning_Rate = rep(c(0.01, 0.01, 0.01, 0.05, 0.05, 0.05, 0.1, 0.1, 0.1), each = 2),
Threshold = rep(c(0.3, 0.5, 0.7, 0.3, 0.5, 0.7, 0.3, 0.5, 0.7), each = 2),
Model = rep(c(“Hebbian”, “Quantum”), 9),
Accuracy = c(0.260, 0.872, 0.261, 0.874, 0.318, 0.871, 0.261, 0.872,
0.260, 0.873, 0.260, 0.873, 0.260, 0.873, 0.261, 0.871,
0.260, 0.873),
Precision = c(0.100, 0.102, 0.099, 0.106, 0.093, 0.103, 0.101, 0.104,
0.100, 0.101, 0.100, 0.103, 0.101, 0.106, 0.101, 0.103,
0.101, 0.106),
Recall = c(0.799, 0.037, 0.798, 0.036, 0.735, 0.037, 0.802, 0.037,
0.801, 0.035, 0.799, 0.035, 0.801, 0.037, 0.801, 0.038,
0.799, 0.038),
F1_Score = c(0.178, 0.053, 0.176, 0.052, 0.165, 0.054, 0.179, 0.054,
0.178, 0.052, 0.177, 0.052, 0.179, 0.054, 0.179, 0.055,
0.178, 0.055)
)
# =============
# 6. Visualization: Bar Charts for Metrics
# ===============
# Define a function to create and save bar charts for a given metric
create_and_save_plot <- function(data, metric, title, filename) {
# Check if the metric exists in the data frame
if (!metric %in% colnames(data)) {
stop(paste(“Metric”, metric, “not found in the data frame.”))
}
# Create the bar chart
p <- ggplot(data, aes(x = factor(Threshold), y = .data[[metric]], fill = Model)) +
geom_bar(stat = “identity”, position = position_dodge(width = 0.8),
width = 0.7, color = “black”) +
facet_wrap(~ Learning_Rate, labeller = label_both) +
labs(title = title, x = “Threshold”, y = metric) +
scale_fill_manual(values = c(“Hebbian” = “white”, “Quantum” = “black”)) +
theme_minimal() +
theme(
text = element_text(size = 15),
strip.text = element_text(size = 15), # Facet labels
plot.title = element_text(size = 18, hjust = 0.5), # Centered title
legend.title = element_blank(), # Remove legend title
legend.text = element_text(size = 16), # Legend text size
axis.title = element_text(size = 16), # Axis titles
axis.text = element_text(size = 15) # Axis text
)
# To ensure white bars are visible, set a light gray background
p <- p + theme(
panel.background = element_rect(fill = “grey90”, color = NA),
plot.background = element_rect(fill = “grey95”, color = NA)
)
# Save the plot as a high-resolution PNG file
ggsave(filename, plot = p, width = 8.5, height = 11, dpi = 500, units = “in”, device = “png”)
# Optionally, display the plot in the R session
print(p)
}
# Define metrics and corresponding filenames
metrics_info <- list(
list(metric = “Accuracy”, title = “Accuracy Comparison for Hebbian and Quantum-Inspired Models”, filename = “Figure3_Accuracy.png”),
list(metric = “Precision”, title = “Precision Comparison for Hebbian and Quantum-Inspired Models”, filename = “Figure4_Precision.png”),
list(metric = “Recall”, title = “Recall Comparison for Hebbian and Quantum-Inspired Models”, filename = “Figure5_Recall.png”),
list(metric = “F1_Score”, title = “F1-Score Comparison for Hebbian and Quantum-Inspired Models”, filename = “Figure6_F1_Score.png”)
)
# Iterate through each metric and create/save the corresponding plot
for (info in metrics_info) {
create_and_save_plot(results, info$metric, info$title, info$filename)
}
# ==============
# End of Script
# ==============


